Heat transfer aspect of gaseous slip flows
There exist several operating conditions where gaseous flows behave in a counter-intuitive manner. One important and emerging application area that involves such a flow condition is the development of small scale or miniaturized devices. In such situations, the molecular separation ( λ) becomes comparable with the passage dimension (D), which gives rise to a non-equilibrium condition of the fluid with the wall. The ensuing finite, non-zero velocity at the wall, and temperature difference between fluid and wall cause a deviation in the flow behavior from the established conventional results. This kind of flow is usually encountered with large inlet to outlet pressure ratios because it becomes more difficult to carry widely separated
molecules together. As its consequence, these flows experience strong influence of pressure work leading to expansion cooling. Simultaneously, steep velocity gradients due to miniaturized flow scale manifest as viscous dissipation. Unlike continuum flows, a finite fluid velocity at the wall adds to this viscous dissipation due to finite viscous stress work at the wall. In addition, low Reynolds number (Re) conditions cause axial conduction to dominate appreciably. This heats up the flow even before its entry to the system. Hence, a second wall, upstream of the heating wall is required to quantify the extent of this backward heat penetration. In slip flows, a combination of these factors together defines the flow behavior.
We have analyzed such gaseous flows in the complete slip regime, where Knudsen number in the range (10-5<Kn<10-1) has been covered. To capture the flow physics governed by each of the aforementioned factors, complete set of governing equations for mass, momentum and total energy are solved for the flow of rarefied gaseous nitrogen through a circular pipe. Variation of properties with temperature has been retained. A separate study of low Peclet gaseous flows has also been made to examine explicit response of flow subjected to such conditions. Interesting and useful observations could be drawn from the conducted set of studies.
The complete heating region is found to exhibit two distinct fully developed regions. For the complete flow domain at comparable Kn, the heating region involves significant heating with finite fully developed Nusselt number (Nufd). The second region represents non-heating zone with nearly zero Nufd and the flow field in defined solely by the combined effects of pressure work and viscous dissipation. Flow is found to transfer a considerable portion of the total heat that it receives from the wall towards upstream. This effect increases with rise in wall temperature (Tw) and Kn. As a result, flow experiences enhanced heating with low Peclet (Pe) condition and a shorter length of the flow region to achieve Tw. For this reason, in continuum low Pe conditions, drop in Pe causes a continuous rise Nufd. However, slip flows share their characteristic of non-equilibrium at the wall, which increases with rise in Kn. Hence, a combined effect of axial conduction and slip conditions is displayed by Nufd. It shows a rise till a particular Kn to achieve a maximum, followed by a continuous drop thereafter. This feature is shown in Figure for three different configurations (L/D) ratio. Pe corresponding to different configurations are different. All the three configurations clearly display the complete control of Kn in the range 0.01 <Kn< 0.1 in defining the flow field, whereas in the range 0.001 <Kn< 0.1, both Pe and Kn need to be defined for a complete description of the flow.
Since a large fraction of heat is sent upstream, isothermal and adiabatic upstream wall conditions have been tested. Beyond a limiting Kn (Knlim), the flow is found to experience backward heat propagation up to the inlet, irrespective of the length of the upstream wall supplied. A simple analytical model for the temperature field in the upstream region has been developed to evaluate this Knlim for the given system. This can also be used to evaluate total heat transfer between the wall and fluid which is much larger than what fluid carries downstream with itself. In small scale heat exchangers, it is crucial to know the total heat transfer. It will be predicted erroneously if the conventional approach is followed.
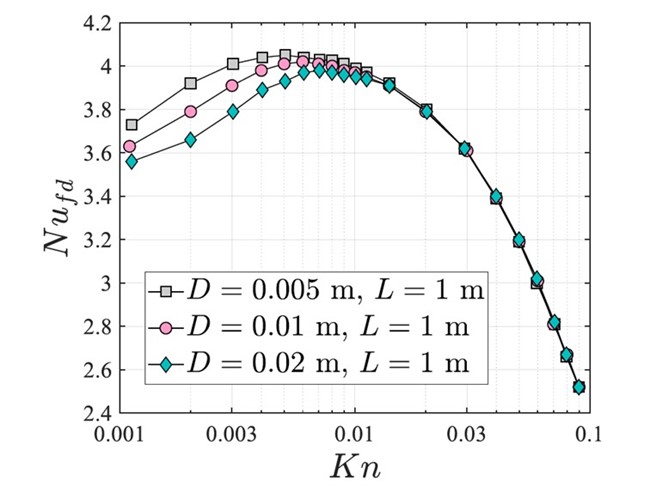Variation of Nufd with Kn for three different configurations of the system
