Grad’s second problem

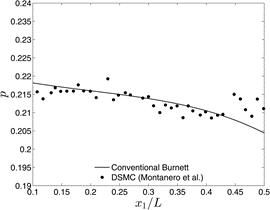
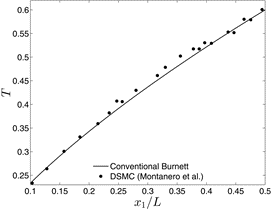
The inadequacy of the celebrated Navier-Stokes equations in describing high Knudsen number flows is well known and documented. This limitation has inspired researchers to search for alternate equations (or higher order continuum transport equations such as Burnett, Grad, OBurnett, etc). However, very few benchmark problems are available in the literature to assess the accuracy of these higher order continuum transport equations.

This important limitation was recognized in our group, and we have proposed the Grad's second problem as a novel benchmark problem. In this problem, we consider the gas to be rest (no bulk velocity) with steady one-dimensional heat flux imposed in the positive x-direction. The interest is in obtaining the ensuing pressure and temperature fields, and comparing these with benchmark data.

The absence of the boundaries, motion and other complications make the test case to be relatively simple. Our work highlights that, surprisingly, only a few of the known higher order continuum transport equations (such as the conventional Burnett equations) yield the correct solution to the problem.

References