A novel iterative approach for solving partial differential equations

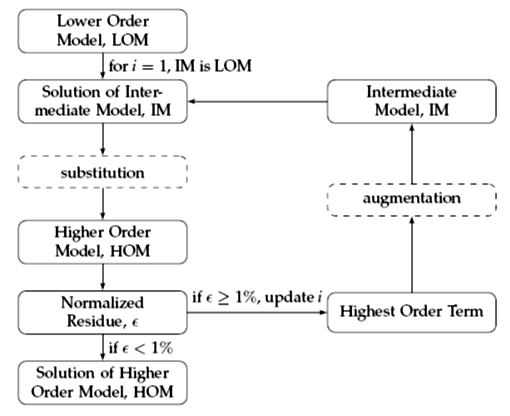
It is not always easy (and often not even possible) to solve partial differential equations analytically; therefore any new method to attack them is welcome. We have proposed a new iterative approach to obtain analytical solution of non-linear partial differential equations. The novelty is in combining physical situation to the mathematical process, during the solution procedure.

The proposed method has been successfully demonstrated for solving the notoriously difficult Burnett equations (which is a superset of the Navier-Stokes equation). The correctness of the solution was demonstrated by showing the equality of the left-hand side to the right-hand side upon substituting the solution into the equation. Since the solution satisfies the governing equation, also boundary conditions, it is deemed to be correct. Two different problems could be solved using this novel approach further attesting to the robustness of the proposed method.

The readers are encouraged to employ this iterative method for their chosen problem – and share their findings with me.

References